Тема1. «Информация и информационные процессы» (9ч)

Урок 8. Алфавитный  подход к определению количества информации

При определении количества информации на основе уменьшения неопределенности наших знаний мы рассматриваем информацию с точки зрения содержания, ее понятности и новизны для человека. С этой точки зрения в опыте по бросанию монеты одинаковое количество информации содержится и в зрительном образе упавшей монеты , и в коротком сообщении "Орел", и в длинной фразе "Монета упала орлом вверх".

Однако при хранении и передаче информации с помощью технических устройств целесообразно отвлечься от содержания информации и рассматривать ее как последовательность знаков (букв, цифр, кодов цветов точек изображения и так далее). Такой подход к количеству информации называется алфавитным.

При алфавитном подходе к определению количества информации отвлекаются  от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы (алфавита). 

Исходя из вероятностного подхода к определению количества информации, набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события).

Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ: 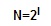, где N — количество знаков в алфавите, I — количество информации.

Информационная емкость знаков зависит от их числа в алфавите (мощности алфавита): чем больше их число, тем большее количество информации несет один знак.

Так, информационная емкость буквы в русском алфавите, если не использовать букву «ё», составляет:

    
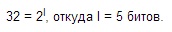
Аналогично легко подсчитать, что каждый знак «алфавита» нервной системы (есть импульс, нет импульса) в соответствии с формулой несет информацию 1 бит, а каждый из четырех символов генетического алфавита (A,G,C,T)— информацию 2 бит.

В двоичной знаковой системе используется всего два символа - 0 и 1. Поэтому, по формуле Хартли получается, что каждый символ несет 1 бит информации.

В соответствии с алфавитным подходом количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на число знаков в сообщении: I=I(знак)*K.

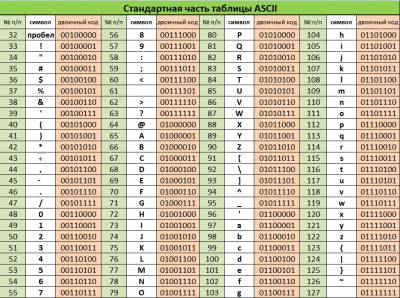
Хотя, как было подсчитано выше, для кодирования буквы в русском алфавите достаточно 5 бит, при кодировании текста в компьютере принято использовать 8 или 16 бит на один символ. Такой выбор обусловлен необходимостью привести к единообразию кодирование символов алфавита любого языка. На предыдущих уроках уже говорилось об таблицах кодирования текста ASCII:

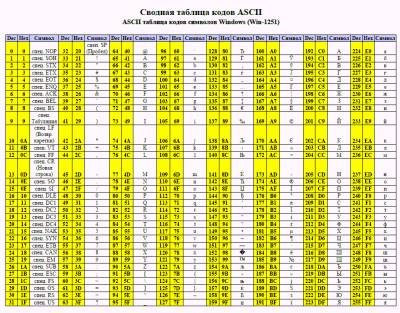
В этой таблице на каждый символ отводится 8 бит: 1 символ = 1 байт. Легко посчитать, что всего можно закодировать 2^8=256 символов. В ASCII первые 32 места - от 0 до 31 - отведены под служебные символы, от 32 до 127 - под символы английского языка, цифры и знаки препинания, а оставшиеся 128 символов - под национальные кодировки. Так, например, выглядит таблица кодировки кириллицы Win1251:

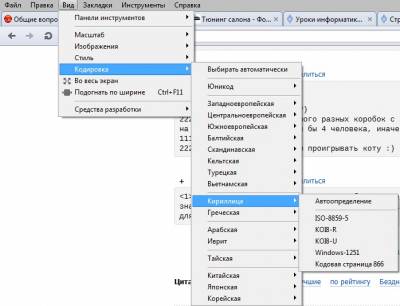
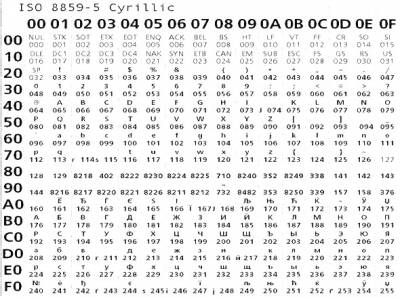
Естественно, что в разных кодировочных таблицах национальные кодировки не совпадают. Это приводит к некорректному отображению текстовых сообщений. Откройте браузер и смените тип кодировки: 

Вы увидите, что текст превратится в набор нечитаемых символов. Чтобы этого избежать, была разработана единая кодировка текста UNICODE. В ней каждый символ кодируется 16 битами: 1 символ=2 байта.

Поэтому, чтобы рассчитать объем текстового сообщения в компьютере, нужно знать способ кодировки текста: ASCII - 1 символ=1 байт, UNICODE - 1 символ=2 байта

Контрольные вопросы:

1. Какое из сообщений имеет больший информационный объем: слово из 5 символов на русском языке или слово из 5 символов на китайском языке?

2. Какое количество информации несет двоичный код 11010011?

3. Каким наименьшим количеством бит можно закодировать арабские цифры?

4. Какова информационная емкость сообщения: 

Минимальная единица измерения информации 1 бит

если а) каждый символ закодирован минимальным количеством бит;

б) для кодировки использовалась таблица ASCII;

в) сообщение закодировано в UNICODE.